旋转矩阵中的6保6公式是数学与工程应用相结合的完美体现。在三维空间中，一个物体进行旋转时，其位置、方向和姿态等六个自由度（即三个平移自由度和三个旋转自由度）在旋转过程中保持不变，这就是所谓的“6保6”原则。，，在数学上，6保6公式可以通过旋转矩阵来描述。一个物体在三维空间中的旋转可以看作是绕某个轴的旋转，而这个旋转可以用一个3x3的旋转矩阵来表示。该矩阵的六个元素（即三个旋转角和三个旋转轴）在旋转过程中保持不变，这就是6保6公式的数学表达。，，在工程应用中，6保6公式被广泛应用于机器人学、计算机视觉、航空航天等领域。在机器人学中，通过使用6保6公式可以精确地控制机器人的姿态和运动轨迹；在计算机视觉中，可以用于三维重建和图像配准等任务；在航空航天中，可以用于飞行器的姿态控制和导航等任务。，，6保6公式是数学与工程应用相结合的典范，它不仅在理论上具有重要意义，而且在实践中也具有广泛的应用价值。

在数学与工程学的交汇处，旋转矩阵以其独特的魅力和强大的功能，在众多领域中扮演着不可或缺的角色，特别是在三维空间变换、图像处理、机器人学以及计算机视觉等领域，旋转矩阵不仅是理论研究的基石，也是实际工程应用中不可或缺的工具，而“6保6”公式，作为旋转矩阵中一个重要的概念，更是将这一数学工具的实用性和精确性推向了新的高度，本文将深入探讨“6保6”公式的原理、应用及其在工程实践中的价值。

一、旋转矩阵的基础概念

在三维空间中，任何物体的旋转都可以通过绕某一点和某一轴的旋转来描述，为了在数学上精确表示这种旋转，我们引入了旋转矩阵，旋转矩阵是一种特殊的正交矩阵，它能够通过线性变换将一个坐标系下的向量映射到另一个与之仅通过旋转相区别的坐标系中。

一个绕Z轴的旋转可以由以下形式的矩阵表示：

\[ R_z(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \]

$\theta$ 是旋转的角度，类似地，绕X轴和Y轴的旋转矩阵分别为：

\[ R_x(\theta) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{bmatrix} \]

\[ R_y(\theta) = \begin{bmatrix} \cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \end{bmatrix} \]

这些矩阵的引入，使得我们能够以数学的方式精确描述和计算三维空间中的旋转操作。

二、“6保6”公式的提出与意义

“6保6”公式是针对三维空间中任意轴向的旋转提出的一种简化计算方法，在三维空间中，任意轴的旋转可以通过绕Z轴的三次连续旋转来等效表示，这三次旋转分别对应于绕Z轴的偏航（Yaw）、俯仰（Pitch）和滚转（Roll）三个角度，这种表示方法不仅在理论上简化了计算过程，还在实践中极大地提高了效率。

“6保6”公式的核心在于：通过三个独立的旋转角度（即偏航角、俯仰角和滚转角），可以完全确定一个物体在三维空间中的任意方向和姿态，这种表示方法之所以被称为“6保6”，是因为它用六个自由度（三个角度）来描述一个物体在三维空间中的六个方向上的变化。

三、“6保6”公式的具体应用

1、机器人学与运动控制：在机器人学中，机器人的姿态控制是一个关键问题，通过“6保6”公式，可以精确地计算和调整机器人的方向和位置，实现精准的路径规划和运动控制，在无人机飞行控制中，利用“6保6”公式可以确保无人机在复杂环境中的稳定飞行和精确转向。

2、计算机视觉与图像处理：在计算机视觉中，对图像进行旋转、缩放和倾斜等操作是常见的需求。“6保6”公式为这些操作提供了数学上的基础，使得图像处理算法能够更加高效和精确地执行，在人脸识别和图像配准等应用中，“6保6”公式帮助实现了对图像的精确对齐和旋转校正。

3、航天与导航系统：在航天和导航系统中，对航天器的精确控制和姿态调整至关重要。“6保6”公式为这些系统提供了一种有效的数学模型，使得航天器能够在复杂的宇宙环境中保持正确的姿态和方向，在卫星的轨道控制和姿态调整中，“6保6”公式确保了卫星能够按照预定的轨迹和姿态进行运动。

4、游戏开发：在游戏开发中，“6保6”公式被广泛应用于角色的动画制作、相机控制和场景布置等方面，通过精确的旋转计算，游戏开发者能够创造出逼真且流畅的视觉效果，提升玩家的游戏体验。

四、“6保6”公式的数学推导与实现

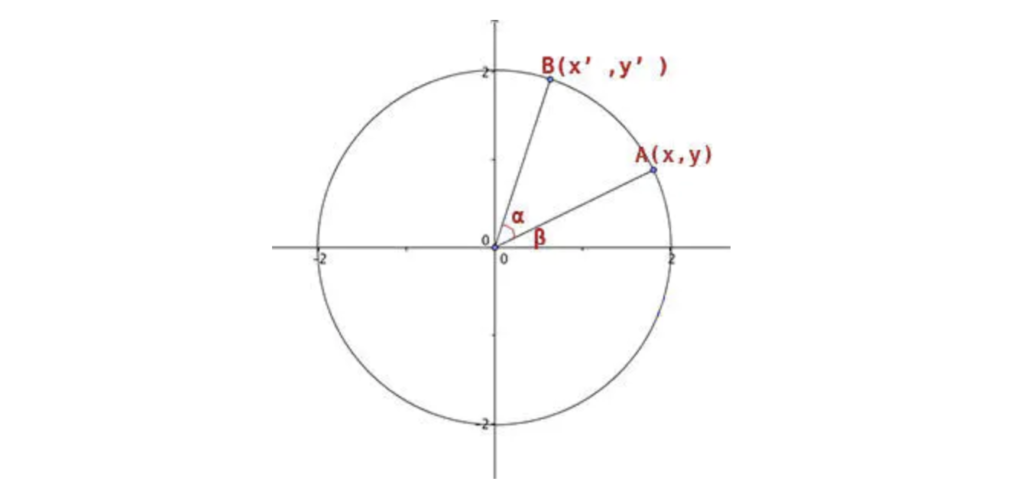
“6保6”公式的数学推导基于欧拉角的概念，即任何三维空间的旋转都可以通过绕三个互相垂直的轴（X、Y、Z）的连续旋转来合成，对于一个绕任意轴$\mathbf{n} = (n_x, n_y, n_z)$的旋转角度$\theta$，可以通过以下步骤进行计算：

1、首先绕Z轴旋转一个角度$\alpha$，使得新的Z轴与$\mathbf{n}$的Z分量对齐；

2、然后绕新的X轴（即原来的$\mathbf{n}$方向）旋转一个角度$\beta$；

3、最后绕Z轴再旋转一个角度$\gamma$，以完成最终的旋转。

这一系列操作对应的旋转矩阵可以通过一系列的矩阵乘法得到，具体形式较为复杂但可以通过数学软件或编程语言进行计算和实现。

五、“6保6”公式的优势与挑战

优势：

简洁性：“6保6”公式以最少的参数（三个角度）描述了三维空间中的任意旋转，大大简化了计算过程。

实用性：该公式在工程实践中具有广泛的应用，从机器人控制到图像处理，从航天导航到游戏开发，都发挥了重要作用。

直观性：通过三个基本动作（偏航、俯仰、滚转）的组合，使得旋转操作更加直观易懂。

挑战：

万向锁问题：当使用“6保6”公式时，如果三个欧拉角中有两个角度之和为±90°或±270°，则会出现万向锁现象，导致系统的不稳定，这要求在实际应用中需特别注意角度的选择和限制。

奇异性问题：在某些特定的角度组合下，“6保6”公式的表示方式会变得不唯一或产生歧义，这需要在实际应用中通过额外的约束条件来避免。

精度问题：由于计算过程中的累积误差和舍入误差，“6保6”公式的应用需要特别注意精度控制，尤其是在高精度要求的场合。

六、结论与展望

“6保6”公式作为旋转矩阵中的一个重要概念，不仅在理论上为三维空间中的旋转提供了简洁而有效的表示方法，还在工程实践中发挥了巨大的作用，随着计算机技术和相关领域的发展，“6保6”公式的应用范围将进一步扩大，其精度和效率也将得到进一步提升。“6保6”公式有望在更广泛的领域中得到应用，如虚拟现实、增强现实、自动驾驶等新兴技术领域，为这些技术的发展提供坚实的数学基础和技术支持，随着对万向锁问题和奇异性的深入研究，相信“6保6”公式的应用将更加稳定和可靠，为解决更多复杂问题提供强有力的工具。